Someone Built An Engine Crane Out Of Wood. Let's Do Math To See If It's Safe
Owning a car can be hard, but it's the people who brave the struggle who do the most for car culture. Among those people is this hero in Seattle who built an engine crane out of two-by-six planks. It's incredible. But, let's look into how safe it is.
I have nothing more than the photo above to go on, so this whole article is a largely pointless exercise in figuring out how strong some random dude's wood crane is, even though I have no clue what the load case is. Someone tweeted the image out on Twitter, and told me in a private message that he saw engine parts all over the road and that the wrencher's "alternator and hood were just laying there."You can see the Audi A6 wagon's alternator under the driver's-side rocker panel, and of course, the hood is leaning up against the rear pillar. Under the car's chin is what appears to be a power steering pump and a bracket or two, presumably for the accessory drive.

A two-by-six wood crane looms over the car's engine bay, with ratchet straps dangling from the overhead beam/gantry spanning from the top of a vertical structure on one side of the Audi to the top of another on the opposite side.
Naturally, you're probably wondering "Is this safe?" Well, I'll reiterate: We don't exactly know what's going on. The running joke among car enthusiasts is that this person is probably yanking the engine to replace a cheap thermostat, since Audis are notoriously hard to work on due to tight under-hood packaging and, frankly, thoughtless engineering.
But I think it's unlikely that the Seattle resident fixing his car in the street plans to lift the entire engine out of the bay. If I had to guess, he's supporting the engine to replace either the engine mounts or something that can't be accessed without removing those mounts. Why is this person not simply supporting the engine using a floor jack on the oil pan with a rubber hockey puck to spread the load? Or, better yet, why isn't this person just using an $80 Harbor Freight Engine Support Bar like the one shown below? (It's probably cheaper than lumber right now. —ED)
I honestly have no clue. But that's not going to stop me from doing a static analysis on whether such a wooden contraption could handle the full weight of the Audi's V6 engine.
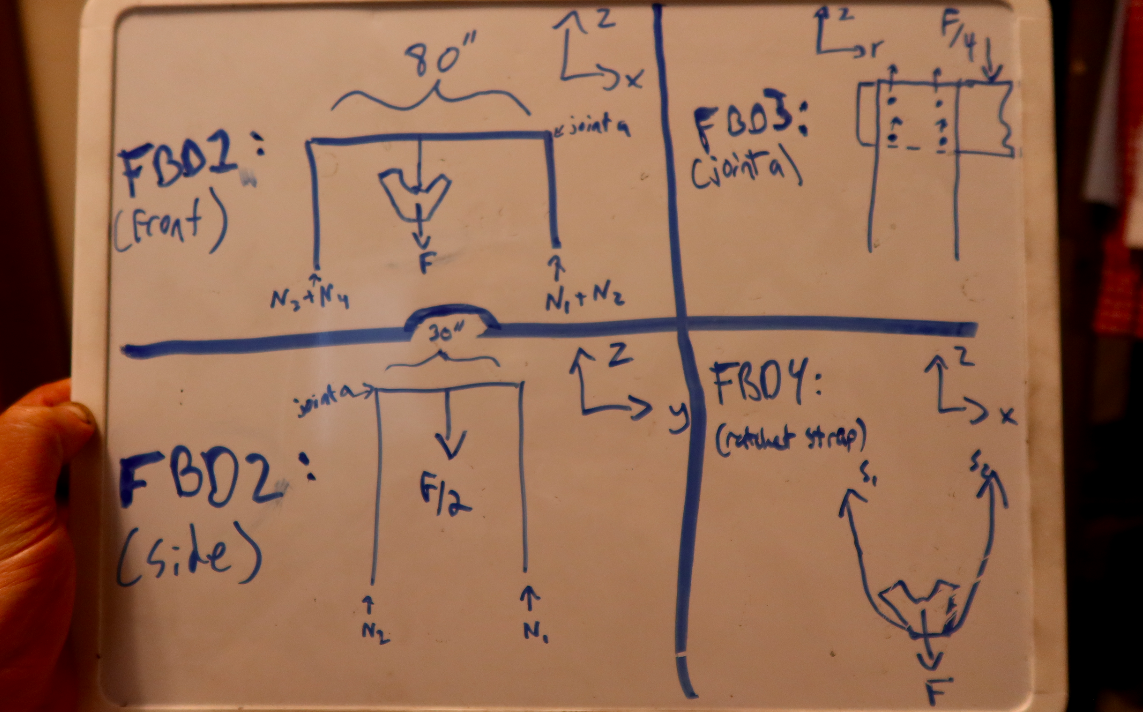
It's been years since I've done a statics problem, so you'll have to bear with me here. The free body diagrams above points out the loads in play. You've got the weight of the motor pulling down on the center of the top square-section crossbeam/gantry and you've got the normal forces/reaction forces of the ground "pushing" up on the four legs. (And that coordinate system at the top right of each diagram? That's just so I don't get called out by other engineers in the comments. I'm sure I'll get called out for something, but it sure as hell won't be due to a lack of a coordinate system).
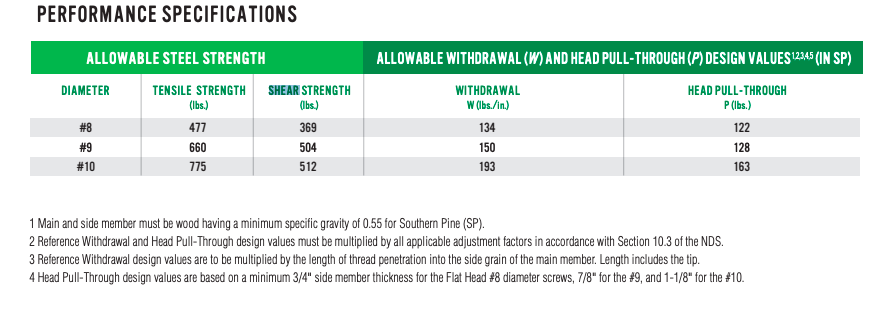
As for stresses, the crossbeam/gantry is seeing bending and shear stresses, the horizontal top members of the vertical structures are also seeing shear and bending stresses, the vertical members on the vertical structures are seeing only compression, and then you've got shear loads on the screws. I'm assuming, based on what I see in the image, that that the builder used four screws per connection.
As for the ratchet strap holding the engine up, I'll assume there's just one looped strap being used, because that little black string doesn't look like it's worth even considering in my calculations.
Anyway, I'm just going to go through these parts one-by-one, and conduct a static analysis to see if this contraption can handle the roughly 400 pound 3.2-liter V6 found in the A6 Avant.

We're going to have to make some assumptions on dimensions. I'll use the fact that the boards are probably two-by-sixes, along with the Audi A6 Avant's dimensions (shown above), to estimate how wide a space that crossmember spans and how far apart and how tall the two vertical members in each vertical structure are.
Anyway, let's start with the pieces closest to the engine and move toward the legs.
The Ratchet Strap
Even a one-inch ratchet strap can handle 400 pounds, so this shouldn't be a huge problem, especially since it's looped. We'll model this as a "pulley problem," which is a typical exercise taught in engineering to help students understand stresses in chains, cables, and straps.
Normally, you'd sum all of the forces in all directions, set that equal to zero (because this system is static, the net force must equal zero. Force equals mass times acceleration. If there's a net force, there must be an acceleration! Since there isn't, the forces must add up to zero), and use the given load and the system geometry to solve for tension in the strap. In this case, the entire load is in the Z direction, so: s1 (strap length one) + s2 (strap length two) – 400 lbs = 0.
We can assume that the two straps carry the load equally (i.e. that the strap can slide where it is joined to the motor, and that friction doesn't lead to one strap carrying most of the load). As such, we find that each strap is seeing only 200 pounds of tension, which is well below the load rating for most ratchet straps.
The Big Crossbeam/Gantry
Let's move to the cross beam/gantry. As you can probably visualize, there are two stresses we need to focus on. There's shear stress, which is just a product of the vertical load trying to get the wood to shear along the Z-axis (as labeled above), and there's also bending stress, which is maximized at the center of the beam (if this thing were to bend and break, it'd crease right there in the middle, as you might imagine).
Calculating shear stress is fairly straightforward. In engineering school, there's something called the "method of sections." You basically make an imaginary cut somewhere along a member, and figure out what the shear and bending loads must be at that cut in order for the system to maintain static equilibrium. The sum of all forces acting on our part must equal zero since there's no acceleration.
We know that at the two points where the beam meets the vertical structure, we're going to see 200 pounds of upward force in order to balance the 400 pound downward load. (I'm going to assume that the engine is being hoisted from exactly the center of the beam; I'm also neglecting the weight of the wood structure itself, since it's relatively low.) That's the calculation you see on the left side in the image above.
If we make a section cut between R1 (where one vertical structure meets the gantry) and the 400 pound load shown above (again, "method of sections"), we find that the shear load in the part anywhere along that section must be 200 pounds to counter the 200 pound load from where the R1 vertical load meets the crossmember.
To translate a shear load into a shear stress, we divide by the cross sectional area of the crossbeam (stress equals force over area), which I'm assuming is a four-by-four piece of wood (and it turns out, a 4x4 is actually 3.5-inches by 3.5-inches). Two hundred divided by the square of 3.5 inches equals 16.3 PSI of shear stress on that crossmember.
Pine wood — and I'm assuming this is yellow pine because it's cheap and available at your local hardware store — tends to have a shear strength of around 1,000 PSI at a minimum (I'll show a table of yellow pine values in a bit), so this is no problem. The 4x4 should be able to handle the shear stresses caused by the 400 pound load.
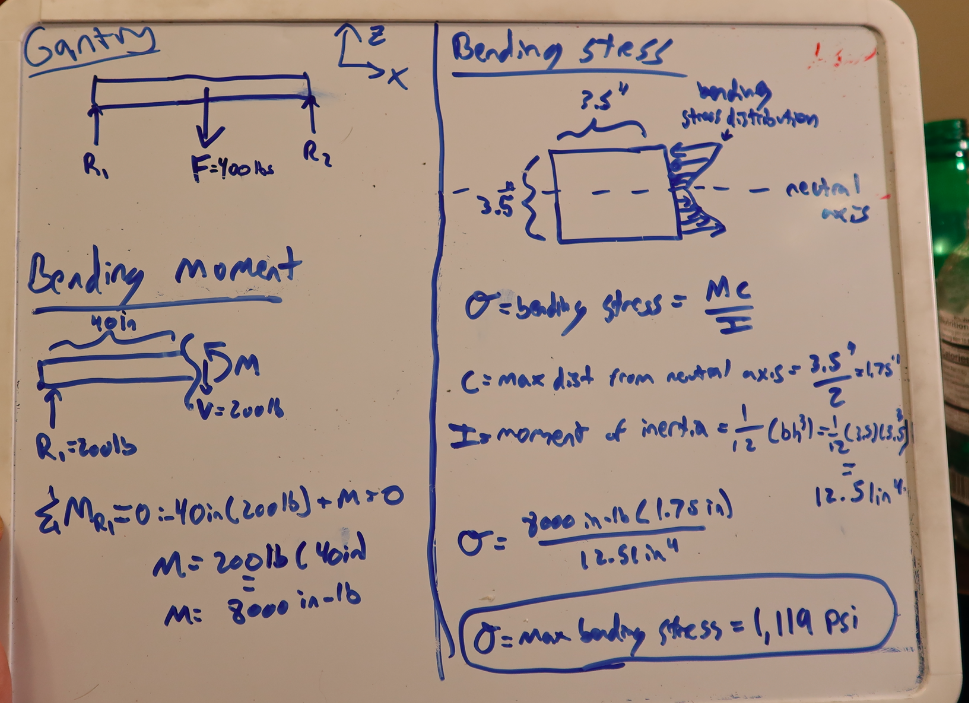
But that's just the shear stress. We also have to calculate the stresses on that beam from the bending load. On the right side of the image above, you'll see the cross section of the top beam, with some arrows drawn to the right side of it. The arrows — taller toward the top and bottom of the beam — show the bending stress distribution. As you load the beam, the extremities of the member are under the most stress. The bottom wants to "separate" from itself, so it's under tension. The top is "pushing" against itself, so it's under compression. At the center of the beam, there's no bending stress at all.
To determine the maximum bending stress on the crossbeam, you could just use the formula below for a "simply supported" beam: (WL/4) where W is the weight of the motor (400 pounds) and L is the length of the beam. Or you could use the method of sections like I did above, and sum all of the moments to zero (because if the moments don't sum to zero, you will get an angular acceleration, and that's not happening — everything is static). In any case, you wind up with 8,000 in-lb of torque due to that engine hanging at the center of an 80-inch beam.
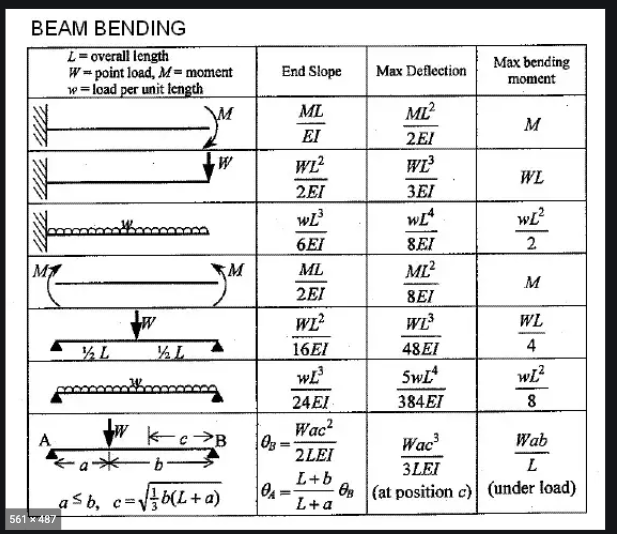
To turn that torque into a stress, you follow the equation: stress equals bending moment times distance from the neutral axis (that's the center of this beam's cross section, where there's no bending stress) divided by moment of inertia (which is just base times height cubed all divided by 12). Anyway, before your eyes glaze over, allow me to just say that I ended up with a maximum of 1,119 PSI of bending stress.
Okay, so that's a huge number compared to 16.32 PSI of shear stress, but will that cause failure?
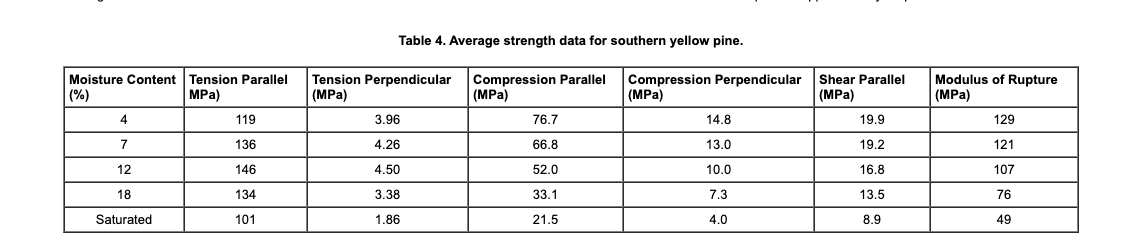
I admittedly am not well-versed on evaluating the strength of wood, as it's more complicated than evaluating metal strength (moisture content and grain direction have huge impacts on strength!). But what I've gathered through some cursory research is that what we want to avoid is reaching the Modulus of Rupture, which Chapter four ("Mechanical Properties of Wood") of the the tome Woodworking Handbook defines thusly:
Modulus of rupture—Reflects the maximum load carrying capacity of a member in bending and is proportional to maximum moment borne by the specimen. Modulus of rupture is an accepted criterion of strength, although it is not a true stress because the formula by which it is computed is valid only to the elastic limit.
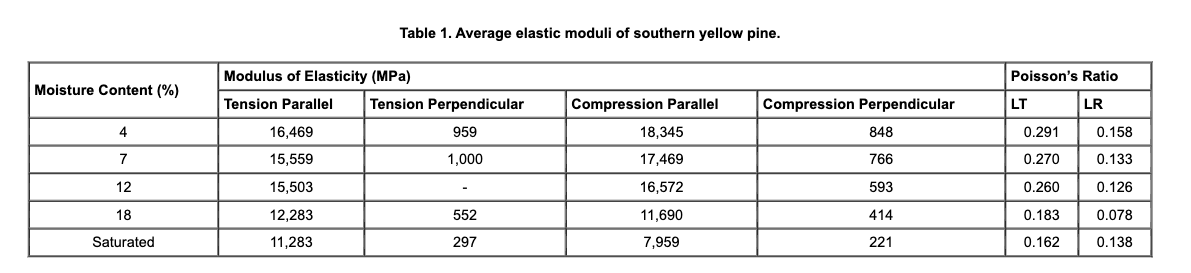
As you can see in the table above, yellow pine has a modulus of rupture that varies quite a bit with moisture content. The drier the wood (up to a certain limit, I'm sure), the stronger. I'm not sure how much moisture a typical 2x6 or 4x4 from Lowes or Home Depot typically has, though I did read about someone online who went out and tested some boards at those two stores to find moisture content roughly between about 10 and 20 percent.
Looking at the Federal Highway Administration's table above (which exists as a study of guardrails, which tend to be mounted on yellow pine posts) and converting to PSI, we find modulii of rupture ranging between roughly 10,000 and 17,000 PSI. So that 1,119 PSI of bending stresses that a 400 pound engine imparted on the middle of an 80-inch 4x4 would, per that table, not be an issue.
The Vertical Supports
Okay so now that we've looked at the shear and bending stresses of the top horizontal member, let's look at compression in the four legs. This one's fairly straightforward. There are four legs supporting 400 pounds, so each leg deals with 100 pounds. Divide that by the cross sectional area of a 2 x 6 (which, it turns out, is actually 1.5-inches by 5.5-inches), and you wind up with a compressive stress of 12.12 psi. That's very little stress whether loaded in parallel or perpendicularly to the grain. For reference, the 4 MPa compressive strength of a fully saturated yellow pine loaded perpendicularly to its grain is still well over 500 PSI.
What about bending on that horizontal 2x6 that spans between the two legs on each side of the car, and that supports the gantry? Let's look at shear and bending stress.
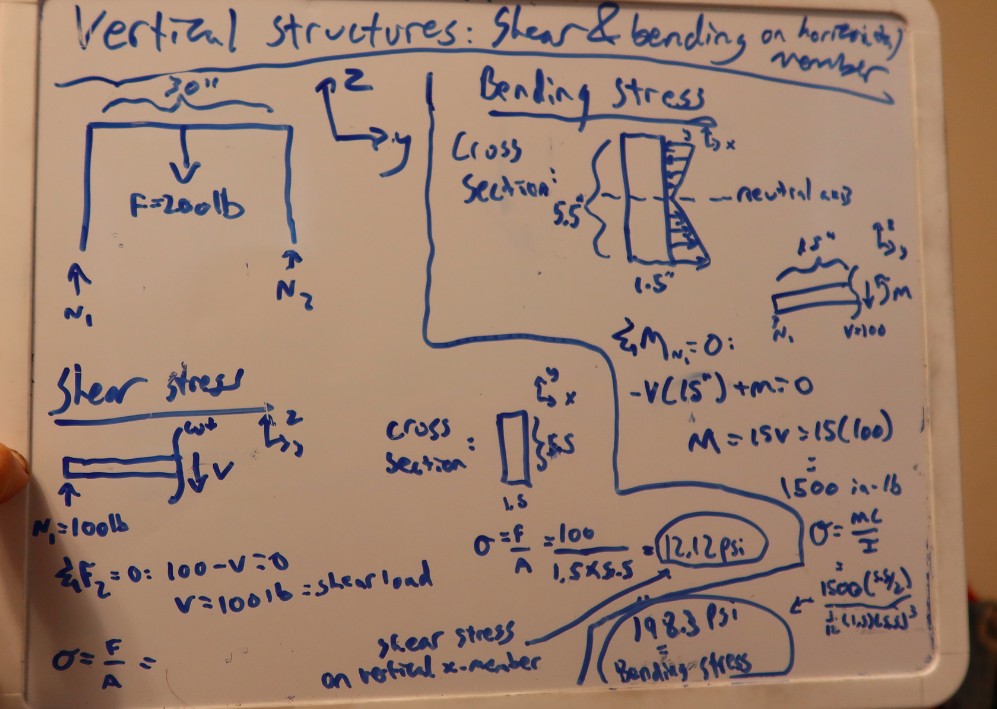
The shear stress, calculated via the "Method of Sections" previously described, is, unsurprisingly, 100 pounds of force. Divide that by the (5.5*1.5) area of a 2x6, and once again, you arrive at 12.12 psi of shear stress. This is a tiny figure compared to the 8.9 to 19.9 MPa (roughly 1,300 PSI to 2,900 PSI) shear strength in the table. The table only shows "Shear parallel [to the grain]," but if you're curious about shear perpendicular to the grain, here's a fun tidbit I found in the Concise Encyclopedia of Composite Materials:
Attempts to obtain shear failure perpendicular to the grain usually result in failure in another failure mode, such as compression perpendicular to the grain. A very limited amount of data suggests that shear strength perpendicular to the grain may be 2.5–3 times that of shear parallel to the grain.
Now let's look at bending loads. Like with the top gantry beam, the bending loads are maximized at the center of the span, which I've estimated to be 30 inches. Taking a section cut, and doing some basic arithmetic, I find that the maximum bending load is 1,500 inch-pounds, which — given the beam's cross-sectional area — translates to around 198.3 PSI of bending stress. That's no big deal. Even a fully saturated pine board has a modulus of rupture of 7,000 PSI. This result shouldn't be surprising given that the 2x6s are mounted in the tall orientation, and that they only span 2.5 feet.
So this member shouldn't fail in bending or shear, and the legs shouldn't fail in compression. The two vertical structures should be strong enough.
Buckling
Let's talk about buckling. Those are some fairly tall, unsupported legs. Could those buckle? To solve this, I need to find Euler's Critical Buckling Stress via the equation below, in which E is the elastic modulus, I is the least moment of inertia for the cross sectional area, and L is the length of the column.
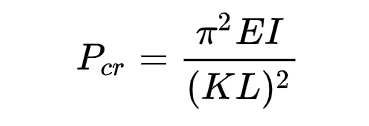
K is a factor used to describe how the beam is fixed. I'm going to assume that the base is fixed (i.e. that there's good traction with the ground) and that the top is free. This gives me a K factor of two (this is just something you find in a table). This, along with some other figures from the federal guardrail study (see below), gives me an answer of 1,770 pounds needed to buckle a six-foot length of 2x6 pine wood. Even if I use lower values for the elastic modulus (Young's modulus) that I've found elsewhere, I still arrive at over 1,000 pounds of force needed to buckle a 2x6 column of pine.
This tells me that buckling isn't an issue.
Okay, so now that I've pointlessly determined that the top 4x4 cross beam is won't fail in shear or bending, and that the vertical structures won't have their legs fail in compression and they won't buckle, and that the horizontal parts of the vertical structures won't shear or fail in bending, it's time to discuss what many of you intuitively know to be true: The legs of this thing are going give out.
The Screws
I'll briefly touch on the screws. The top crossmember of the vertical structures appears to be fastened in single shear. In other words, the screws holding the horizontal support each only have a single shear plane. This means the 200 pound load that this beam is supported, divided by the eight fasteners in use, will be acting on a single cross sectional area of a tiny screw.
This probably won't be an issue, though. Two hundred over eight is only 25 pounds, and damn near any screw can hold over 25 pounds in shear. The Spax screw table above shows what I mean.
What About Stability?
All of these analyses are fun, and it's good to know that, even if this Seattle roadside wrencher were pulling his engine, the ratchet, wood, and screws could handle the stresses.
But let's be honest, there's a bigger issue, here. And I'm not just talking about whatever weird stuff is going on with the car's windows. No, the big issue is that this structure is just unstable, and will have a tendency to want to either rhombus or splay its legs out.
Running calculations for this would require some assumptions about the friction between the legs and the ground, and it'd help if I could carefully measure the exact geometry of the system, because in all of my calculations so far, I've idealized it. And let's be honest: Those vertical structures aren't exactly vertical, and that engine actually appears to be a bit behind the gantry, tending to want to pull the top of the crane towards the car.
But I won't run anymore numbers. My editors are already probably fuming with the fact that I burned an entire day running statics calculations on a wood engine hoist that I spotted on Twitter and that some random dude in Seattle made, probably not even to actually yank his motor, but likely just to support it. This entire article was a waste of everyone's time, if we're being honest, serving an audience of people who needed to know whether this guy's wood crane could hold up to an engine is probably — that is to say: an audience of one.
Anyway, though I won't get into any more figures, I did have a chat with fellow engineer Lewin "TK" Day on Twitter about the crane's unstable equilibrium tending to want it to fold:
Lewin is modeling the ground-to-leg interface as a pin joint, which is fair enough, because they cannot counteract a moment — in other words, since the wood is just sitting on top of the ground, it can't stop itself from wanting to tip.
A crossmember from one vertical structure to another — especially high up and especially diagonally oriented — would help, though I think the big benefit of the crossmember would be preventing the legs from splaying out like this:
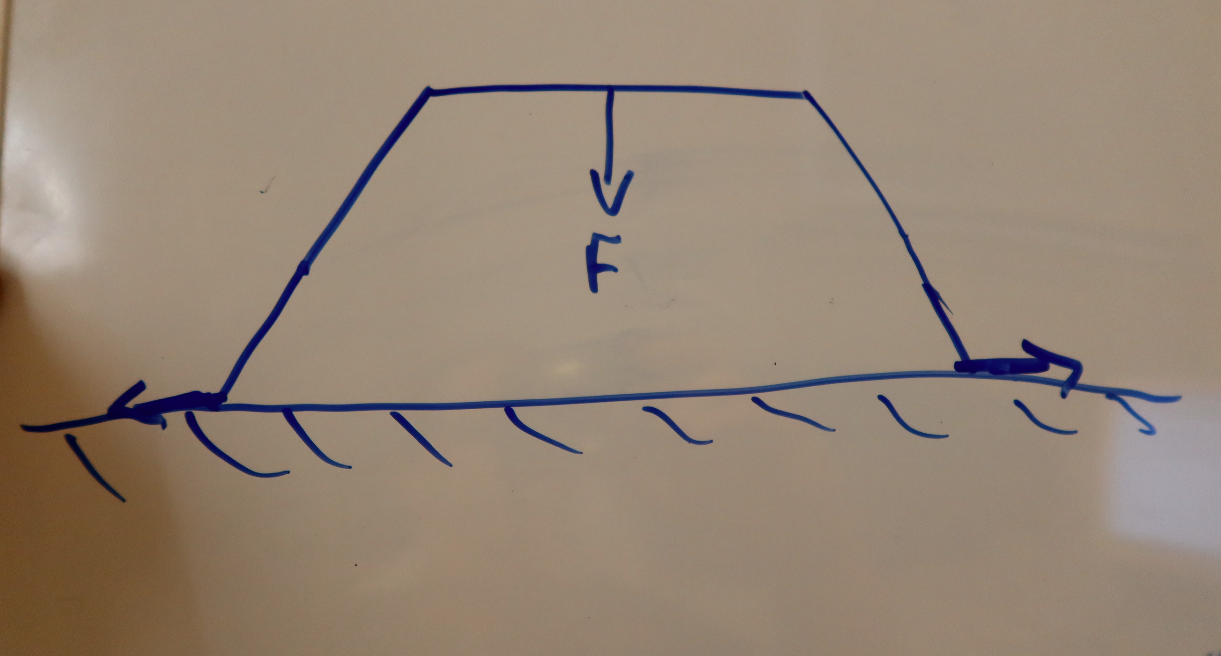
A big weight like a sandbag or cinder block on the outside of each leg would also accomplish the same thing.
Anyway, the takeaway here is that this crane, with a few modifications, would probably work fine for yanking a 400 pound motor. Should you try that and put my rusty statics skills to the test? Absolutely not.